Simpson´s rule is a numerical integration technique that avoids finding a solution for a definite
integral using geometric interpretation. The idea is to find a numeric value, which will be approximated.
In other words, to find :
Geometric
considerations for the rule.
Using the
application of integration, which is an area under a curve; Simpson´s rule
proposes to make a new curve from three points that are in the function. They are
f(a), f(b) and f((a+b)/2), as the graphic expresses. The last one means the
middle point between to the others.
The objective
to make a new curve, with a degree over 1, is that it will be closer to
the real curve f(x).
To make the
new curve, Simpson used interpolation method, which consists of finding a function
that is more approximated to some points on the plan. They could represent
phenomena, statistics, measurements, etc.
After defining
the parabola, we have to calculate the area under it using the traditional
method. In other words, integrate the approximated polynomial.
Simpson´s
formula is:
In general that formula comes from the integration of ax² + bx + c, it is evaluated from –h to h. Like the next
image shows. For practical purposes we are not going to explain where the
formula comes from.
To increase the precision and decrease the error makes
between f(x) function and the parabola, we imagine that we can divide the
section to evaluate in n parts and the sum of all of them will be more approximated
to the real area. The bigger the number of parts, the more approximated
is the area. The measure of these parts is going to be proposed or calculated
by the formula ((a-b)/n) where n is a proposed number, which refers to the number
of parts you are going to divide de evaluated section. Do not forget that all
the parts measure the same.
 |
|
The yellow lines represent the total area. The blue ones
are the error. Most of it is offset.
|
 |
| Division of the total area in sections. Each one is defined by x0 and x1,where dx is the distance between them. Also every one has its own middle point. |
In conclusion we have to use the Simpson´s rule in
each section. To do that we will need do a sum with all the areas. It is important
considering negative areas that means the use of absolute value.
Python thinking
Preliminary ideas:
- Integrate a section´s area.
- Do the calculous general, in other words, do the calculous considering that it will be able to all sections.
- Sum the areas.
- Do not forget the negative areas.
Area of a section.
Through analyzing this graphic we want to calculate area 1, the
replacement of the formula will be in this way:
The replacement came from considering x0 and x1 as integration limits, where dx represents the distance between them, also the middle point is calculated by x1 – (dx/2).
Generic calculation
Once we know how to calculate an area, to finish it
is necessary to do the sum of all of the areas. Therefore if we are thinking in
Python we notice that a cycle is needed, where the iteration variable will be the
superior boundary that is going to take, which starts in a+dx and ends in b. That
is why all of the calculous are considered from the superior boundary. The
Python cycle will be in this way:
Do not you forget to declare the variable suma before
starting the cycle.
Abs means absolute value


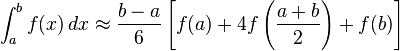





No hay comentarios.:
Publicar un comentario